Abstract
Einstein's vision using quaternions
Events in spacetime and quaternions
Metrics and quaternion products
Physically relevant differential equations
Recreating the Maxwell equations
One unified force field from one potential field
Unified Field equations
Solutions to the unified field equations
Conservation Laws
Transformations of the unified force field
Future Directions

The equations governing gravity and electromagnetism show both profound similarities and unambiguous differences.  Albert Einstein worked to unify gravity and electromagnetism, mainly by trying to generalize Riemannian geometry.  Hamilton's quaternions are a 4-dimensional topological algebraic field related to the real and complex numbers equipped with a static Euclidean 4-basis.  Riemannian quaternions as defined herein explicitly allow for dynamic changes in the basis vectors.  The equivalence principle of general relativity which applies only to mass is generalized because for any Riemannian quaternion differential equation, the chain rule means a change could be caused by the potential and/or the basis vectors.  The Maxwell equations are generated using a quaternion potential and operators.  Unfortunately, the algebra is complicated.  The unified force field proposed is modeled on a simplification of the electromagnetic field strength tensor, being formed by a quaternion differential operator acting on a potential, Box* A*.  This generates an even, antisymmetric-matrix force field for electricity and an odd, antisymmetric-matrix force field for magnetism, where the even field conserves its sign if the order of the differential and the potential are reversed unlike the odd field.  Gauge symmetry is broken for massive particles by the even, symmetric-matrix term, which is interpreted as being due to gravity.  In tensor analysis, a differential operator acting on the field strength tensor creates the Maxwell equations.  The unified field equations for an isolated source are generated by acting on the unified force field with an additional differential operator, Box* Box* A* = 4 pi J.  This contains a quaternion representation of the Maxwell equations, a classical link to the quantum Aharonov-Bohm effect, and dynamic field equations for gravity.  Vacuum and zero net current solutions to the unified field equations are discussed.  The field equations conserve both electric charge density and mass density.  Under a Lorentz transformation, the gravitational and electromagnetic fields are Lorentz invariant and Lorentz covariant respectively, but there are residual terms whose meaning is not clear presently.  An additional constraint is required for gauge transformations of a massive field.  (PACS:12.10.-g)

Three of the four known forces in physics have been unified via the standard model:the electromagnetic, the weak, and the strong forces.  The holdout remains gravity, the first force characterized mathematically by Isaac Newton.  The parallels between gravity and electromagnetism are evident.  Newton's law of gravity and Coulomb's law are inverse square laws.  Both forces can be attractive, but Coulomb's law can also be a repulsive force.  A longstanding goal of modern physics is to explain the similarities and differences between gravity and electromagnetism.  

Albert Einstein had a specific idea for how to formulate an acceptable unified field theory (see Fig. 1, taken from A. Pais, "Subtle is the Lord..." the science and life of Albert Einstein", Claredon Pres, 1982).  One unusual aspect of Einstein's view was that he believed the unified field would lead to a new foundation for quantum mechanics, an idea which is not shared by some of today's thinkers (S. Weinberg, "Dreams of a final theory," Pantheon Books, New York, 1992).  Most of Einstein's efforts over 40 years were directed in a search to generalize Riemannian differential geometry in four dimensions.  

To a degree which has pleasantly surprised the author, Einstein's vision to unify gravity and electromagnetism has been followed.  The construction of a new 4-dimensional geometry is dictated by insights garnered from physics.  Events in spacetime are composed of a scalar for time and a 3-vector for space.  The four-dimensional topological algebraic field of quaternions has the same structure, so quaternions will be the starting point of this effort.  

Laws of physics are expressed in a coordinate-independent way.  The sum or difference of two quaternions can only be defined if the two quaternions in question share the same 4-basis.  Riemannian quaternions make coordinate-independence explicit.  In special relativity, regions in spacetime are delimited by the light cone, where the net change in 3-space is equal to the net change in time.  The parity between changes in 3-space and time is constructed into the definition of a Riemannian quaternion.  In general relativity, the field equations make the metric a dynamic variable.  The basis vectors of Riemannian quaternions can be dynamic, so the metric can be dynamic.  The dynamic nature of the basis vectors leads to the general equivalence principle, whereby any law, even those in electromagnetism, can be the result of a change in reference frame.  

Physical laws are the result of simple Riemannian quaternion differential equations.  First-order Riemannian quaternion differential equations create force fields for gravity, electricity, and magnetism.  Second-order differential equations create dynamic field equations for gravity, the Maxwell equations for electromagnetism, and a classical counterpart to the Aharanov-Bohm effect of quantum mechanics.  Third-order differential equations create conservation laws.  Homogeneous solutions to the second order differential equations are related to gauge symmetry.  

The second paper in this series of three investigates a unified force law, with a focus on a particular solution which may eliminate the need for dark matter to explain the mass distribution and velocity profile for spiral galaxies.  The third paper develops a new approach to quaternion analysis.  The equations of the first two papers are recast with the new definition of a quaternion derivative, resulting in a quantum unified field and force theory.  

An event in spacetime is considered by the author as the fundamental form of information in physics.  Events have structure.  There are four degrees of freedom divided into two dissimilar parts:time is a scalar, and space is a 3-vector.  This structure should be reflected in all the mathematics used to describe patterns of events.  For this reason, this paper focuses exclusively on quaternions, the 4-dimensional number where the terms scalar and vector where first used.  

Hamilton's quaternions, along with the far better know real and complex numbers, can be added, subtracted, multiplied and divided.  Technically, these three numbers are the only finite-dimensional, associative, topological, algebraic fields, up to an isomorphism (L. S. Pontryagin, "Topological groups, translated from the Russian by Emma Lehmer, Princeton University Press, 1939).  Properties of these numbers are summarized in the table below by dimension, if totally ordered, and if multiplication commutes:

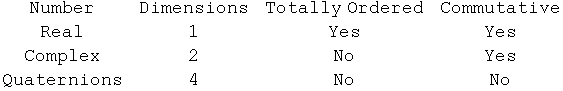
Hamilton's quaternions have a Euclidean 4-basis composed of 1, i, j, and k.  The rules of multiplication were inspired by those for complex numbers: 1^2=1, i^2=j^2=k^2=ijk=-1.  Quaternions also have a real 4x4 matrix representation:

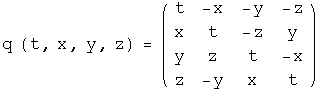
Although written in Cartesian coordinates, quaternions can be written in any linearly-independent 4-basis because matrix algebra provides the necessary techniques for changing the basis.  Therefore, like tensors, a quaternion equation is independent of the chosen basis.  One could view quaternions as tensors restricted to a 4-dimensional algebraic field.  For the sake of consistency, all transformations are also constrained to the same division algebra.  This constraint might first appear too restrictive since for example it eliminates simple matrices for row permutations.  Since quaternions are an algebraic field, there necessarily exists a combination of quaternions that achieves the action of a permutation.  The need for consistency will overrule convenience.  

Laws in physics are independent of coordinate systems.  To make the coordinate independence explicit, amplitudes and basis vectors will be separated using a new notation.  Consider a quaternion 4-function, A_n=(a_0, a_1, a_2, a_3), and an arbitrary 4-basis, Ihat_n=(ihat_0, ihat_1, ihat_2, ihat_3).  In spacetime, the line that divides causality is define by the light cone.  On the light cone, the total change in 3-space over the change in time is equal to one.  Physics therefore indicates parity between the total 3-vector and the scalar, instead of weighing all four equally.  A coordinate-independent Riemannian quaternion is defined to be A_0 Ihat_n=(a_0 ihat_0/3, a_1 ihat_1/3, a_2 ihat_2/3, a_3 ihat_3/3).  The scaling factor of a third for the 3-vector plays a vital role in the definition of a regular function in the third paper of this series.  

The equivalence principle of general relativity asserts, with experiments to back it up, that the inertial mass equals the gravitational mass.  An accelerated reference frame can be indistinguishable from the effect of a mass density.  No corresponding principle applies to electromagnetism, which depends only on the electromagnetic field tensor built from the potential.  With Riemannian quaternions, the 4-unit vector does not have to be static, as illustrated by taking the time derivative of the first term and using the chain rule:

The unit vector for time, ihat_0, can change over an infinitely small amount of time, i_0.  Any change in a quaternion potential function could be due to contributions from a change in potential, the ihat_0 da_0/di_0 term, and/or a change in the basis, the a_0 dihat_0/di_0 term.  Is this mathematical property related to physics? Consider Gauss' law written with Riemannian quaternions:

The divergence of the electric field might equal the source, or equivalently, the divergence of the basis vectors.  The "general equivalence principle" as defined here means that any measurement can be due to a change in the potential and/or a change in the basis vectors.  The general equivalence principle is applicable to both gravity and electromagnetism.  

The theories of special and general relativity dictate the distance between events in spacetime.  Although fundamentally different in their mathematical structure, inertia is a link between the two.  Special relativity dictates the transformation rules for observers who change their inertia, assuming the system observed does not change.  The field equations of general relativity detail the changes in distance due to a system changing its inertia from the vacuum to a non-zero energy density.  A quaternion product necessarily contains information about the metric, but also has information in the 3-vector.  This additional information about quaternion products will suggest a provocative link between metrics and inertia consistent with both special and general relativity.  

Most structures in Nature do not transform like a scalar and a 3-vector.  Quaternion products multiply two 4-basis vectors, and those products will transform differently.  The rules of quaternion multiplication mirror those of complex numbers.  Instead of the imaginary number i, there is a unit 3-vector for each quaternion playing an analogous role.  The difference is that unit 3-vectors do not all have to point in the same direction.  Based on the angle between them, two different unit 3-vectors have both a dot and cross product.  The dot and cross products completely characterize the relationship between the two unit vectors.  Compare the product of multiplying two complex numbers (a, bi) and (c, di):

with two quaternions, (a, B ) and (c, D ),

Complex numbers commute because they do not have a cross product in the result.  If the order of quaternion multiplication is reversed, then only the cross product would change its sign.  Quaternion multiplication does not commute due to the behavior of the cross product.  If the cross product is zero, then quaternion multiplication has all of the properties of complex numbers.  If, on the other hand, the only value of a quaternion product is equal to the cross product, then multiplication is anti-commutative.  Individually, the mathematical properties of commuting and anti-commuting algebras are well known.  A quaternion product is the superposition of these two types of algebras that forms a division algebra.  

Several steps are required to square of the difference of two Riemannian quaternions to form a measure of distance.  First, the basis of the two quaternions must be shared.  It makes no sense to subtract something in spherical coordinates from something in Cartesian coordinates.  The basis does not have to be constant, only shared.  Every quaternion commutes with itself, so the cross product is zero.  There are seven unique pairs of basis vectors in a square:

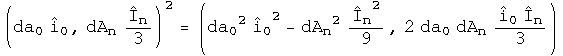
The signs were chosen to be consistent with Hamilton's quaternion algebra.  The four square basis vectors i_mu^2 define the metric.  If the basis vectors are not constant, then the metric is dynamic.  Define a "3-rope" to be the three other terms, which have the form i_0 I_n.  Notice that the 3-rope starts in one time-space location and will have a non-zero length if it ends up at a different location and time.  With quaternion products, the 3-rope is a natural companion to a metric for information about distance.  

In special relativity, if the inertia of the observer but not the system is changed, the metric is invariant.  The 3-rope is covariant, because it is known how it changes.  Given the utility of duality, a complementary hypothesis to the invariant metric of special relativity would propose the if the inertia of the system but not the observer is changed, there exists a choice of basis vectors such that the 3-rope is invariant but the metric changes in a known way.  This could be written in algebraically using the following rule:

If the magnitude of the time and 3-space basis vectors are inversely related, the magnitude of the product of the time basis vector with each 3-space basis vector will be constant even if the basis vectors themselves are dynamic.  This hypothesis asserts the existence of such a basis, but that particular basis does not have to be used.  

Hamilton had the freedom to use the rule found in the above equation, but made the more obvious choice of i_0^2 = -I_n^2.  The existence of a basis where the 3-rope is constant despite a change in the inertia of the system will have to be treated as provisional in this paper.  In the second paper of this series, a metric with this property will be found and discussed.  

Is there a rational way to construct physically relevant quaternion equations? The method used here will be to mimic the tensor equations of electromagnetism.  The electromagnetic field strength tensor is formed by a differential operator acting on a potential.  The Maxwell equations are formed by acting on the field with another differential operator.  The Lorentz 4-force is created by the product of a electric charge, the electromagnetic field strength tensor, and a 4-velocity.  This pattern will be repeated starting from an asymmetric field to create the same field and force equations using quaternion differentials and potentials.  The challenge in this exercise is in the interpretation, to see how every term connects to established laws of physics.  

As a first step to constructing differential equations, examine how the differential operator (d/dt, Del) acts on a potential function (phi, A):

For the sake of clarity, the notation introduced for Riemann quaternions has been suppress, so the reader is encouraged to recognize that there are also a parallel set of terms for changes in the basis vectors.  The previous equation is a complete assessment of the change in the 4-dimensional potential/basis, involving two time derivatives, the divergence, the gradient and the curl all in one.  A unified field theory should account for all conceivable forms of change in a 4-dimensional potential/basis, as is the case here.

Quaternion operators and potentials have not been used to express the Maxwell equations.  The reason can be found in the previous equation, where the sign of the divergence of A is opposite of the curl of A.  In the Maxwell equations, the divergence and the curl involving the electric and magnetic field are all positive.  Many others, even in Maxwell's time, have used complex-valued quaternions for the task because the extra imaginary number can be used to get the signs correct.  However, complex-valued quaternions are not an algebraic field.  The norm, t^2+x^2+y^2+z^2, for a non-zero quaternion could equal zero if the values of t, x, y, and z were complex.  This paper involves the constraint of working exclusively with 4-dimensional algebraic fields.  Therefore, no matter how salutary the work with complex-valued quaternions, it is not relevant to this paper.

The reason to hope for unification using quaternions can be found in an analysis of symmetry provided by Albert Einstein:

"The physical world is represented as a four-dimensional continuum.  If in this I adopt a Riemannian metric, and look for the simplest laws which such a metric can satisfy, I arrive at the relativistic gravitation theory of empty space.  If I adopt in this space a vector field, or the antisymmetric tensor field derived from it, and if I look for the simplest laws which such a field can satisfy, I arrive at the Maxwell equations for free space." [einstein1934]

The "four-dimensional continuum" could be viewed as a technical constraint involving topology.  Fortunately, quaternions do have a topological structure since they have a norm.  Nature is asymmetric, containing both a symmetric metric for gravity and an antisymmetric tensor for electromagnetism.  With this in mind, rewrite out the real 4x4 matrix representation of a quaternion:

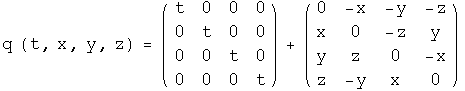
The scalar component (t in representation above) can be represented by a symmetric 4x4 matrix, invariant under transposition and conjugation (these are the same operations for quaternions).  The 3-vector component (x, y and z in the representation above) is off-diagonal and can be represented by an antisymmetric 4x4 matrix, because taking the transpose will flip the signs of the 3-vector.  Quaternions are asymmetric in their matrix representation, a property which is critical to using them for unifying gravity and electromagnetism.

Maxwell speculated that his set of equations might be expressed with quaternions someday (J. C. Maxwell, "Treatise on Electricity and Magnetism," Dover reprint, third edition, 1954).  The divergence, gradient, and curl were initially developed by Hamilton during his investigation of quaternions.  For the sake of logical consistency, any system of differential equations, such as the Maxwell equations, that depends on these tools must have a quaternion representation.

The Maxwell equations are gauge invariant.  How can this property be built into a quaternion expression? Consider a common gauge such as the Lorenz gauge, dphi/dt + div A = 0.  In quaternion parlance, this is a quaternion-scalar formed from a differential quaternion acting on a potential.  To be invariant under an arbitrary gauge transformation, the quaternion-scalar must be set to zero.  This can be done with the vector operator, (q-q*)/2.  Search for a combination of quaternion operators and potentials that generate the Maxwell equations:

This is Ampere's law and the no monopoles vector identity (assuming a simply-connected topology).  Any choice of gauge will not make a contribution due to the vector operator.  If the vector operator was not used, then the gradient of the symmetric-matrix force field would be linked to the electromagnetic source equation, Ampere's law.

Generate the other two Maxwell equations:

This is Gauss' and Faraday's law.  Again, if the vector operator had not been used, the time derivative of the symmetric-matrix force field would be associated with the electromagnetic source equation, Gauss' law.  To specify the Maxwell equations completely, two quaternion equations are required, just like the 4-vector approach.

Although successful, the quaternion expression is unappealing for reasons of simplicity, consistency and completeness.  A complicated collection of sums or differences of differential operators acting on potentials - along with their conjugates - is required.  There is no obvious reason this combination of terms should be central to the nature of light.  One motivation for the search for a unified potential field involves simplifying the above expressions.

When a quaternion differential acts on a function, the divergence always has a sign opposite the curl.  The opposite situation applies to the Maxwell equations.  Of course the signs of the Maxwell equations cannot be changed.  However, it may be worth the effort to explore equations with sign conventions consistent with the quaternion algebra, where the operators for divergence and curl were conceived.

Information about the change in the potential is explicitly discarded by the vector operator.  Justification comes from the plea for gauge symmetry, essential for the Maxwell equations.  The Maxwell equations apply to massless particles.  Gauge symmetry is broken for massive fields.  More information about the potential might be used in unification of electromagnetism with gravity.  A gauge is also matrix symmetric, so it could provide a complete picture concerning symmetry.

For massless particles, the Maxwell equations are sufficient to explain classical and quantum electrodynamic phenomena in a gauge-invariant way.  To unify electromagnetism with gravity, the gauge symmetry must be broken, opening the door to massive particles.  Because of the constraints imposed by quaternion algebra, there is little freedom to choose the gauge with a simple quaternion expression.  In the standard approach to the electromagnetic field, a differential 4-vector acts on a 4-vector potential in such a way as to create an antisymmetric second-rank tensor.  The unified field hypothesis proposed involves a quaternion differential operator acting on a quaternion potential:

This is a natural suggestion with this algebra.  The antisymmetric-matrix component of the unified field has the same elements as the standard electromagnetic field tensor.  Define the electric field E as the even terms, the ones that will not change signs if the order of the differential operator and the potential are reversed.  The magnetic field B is the curl of A, the odd term.  The justification for proposing the unified force field hypothesis rests on the presence of the electric and magnetic fields.

In some ways, the above equation looks just like the old idea of combining a scalar gauge field with the electromagnetic field strength tensor, as Gupta did in 1950 in order to quantize the Maxwell equations.  He concluded that although useful because it is written in manifestly relativistic form, no new results beyond the Maxwell equation are obtained.  Examine just the gauge contribution to the Lagrangian for this unified field:

Take the derivative of the Lagrangian with respect to the gauge variables:

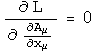
By Noether's theorem, this conserved current indicates a symmetry of the Lagrangian.  This is why the proposal involves new physics.  The gauge is a dynamic variable constrained by the Lagrangian.  

A quaternion potential function has four degrees of freedom represented by the scalar function phi and the 3-vector function A.  Acting on this with one[or more] differential operators does not change the degrees of freedom.  Instead, the tangent spaces of the potential will offer more subtle views on the rules for how potentials change.  

The three classical force fields, g, E, and B, depend on the same quaternion potential, so there are only four degrees of freedom.  With seven components to the three classical force fields, there must be three constraints between the fields.  Two constraints are already familiar.  The electric and magnetic field form a vector identity via Faraday's law.  Assuming spacetime is simply connected, the no monopoles equation is another identity.  A new constraint arises because both the force fields for gravity and electricity are even.  It will be shown subsequently how the even force fields can partially constructively or destructively interfere with each other.  

In the standard approach to generating the Maxwell equations, a differential operator acts on the electromagnetic field strength tensor.  A unified field hypothesis for an isolated source is proposed which involves a differential quaternion operator acting on the unified field:

This second order set of four partial differential equations has four unknowns so this is a complete set of field equations.  Rewrite the equations above in terms of the classical force fields:

The unified field equations contain three of the four Maxwell equations explicitly:Gauss' law, the no magnetic monopoles law, and Ampere's law.  Faraday's law is a vector identity, so it is still true implicitly.  Therefore, a subset of the unified field equations contains a quaternion representation of the Maxwell equations.  The justification for investigating the unified field equation hypothesis is due to the presence of the Maxwell equations.  

There is a very simple relationship between Faraday's law and the equation above.  All that needs to be done is to subtract twice the time derivative of the magnetic field from both sides.  What does this do to the 4-vector current density J? Now there is a current that transforms like a pseudo-current density, making the proposal more complete.  The volume integral of this pseudo-current density is the total magnetic flux:

The unified field equation postulates a pseudo 3-vector current composed of the difference between the time derivative of the magnetic field and the curl of the electric field.  The Aharonov-Bohm effect depends on the total magnetic flux to create changes seen in the energy spectrum.[aharonov1959] The volume integral of the time derivative of the magnetic field is a measure of the total magnetic flux.  The pseudo-current density is quite unusual, transforming differently under space inversion than the electric current density.  One might imagine that a Lorentz transformation would shift this pseudo-current density into a pseudo-charge density.  This does not happen however, because the vector identity involving the divergence of a curl still applies.  The Aharonov-Bohm phenomenon, first viewed as a purely quantum effect, may have a classical analogue in the unified field equations.

The constants used here were chosen to suggest a connection to the Aharonov-Bohm (Y Aharonov and D. Bohm, "Significance of electromagnetic potentials in the quantum theory," Phys. Rev, 115:485-491, 1959).  The Aharonov-Bohm effect depends on the total magnetic flux to create changes seen in the energy spectrum.  A pseudo-current density is unusual, transforming differently under space inversion than the electric current density.  One might imagine that a Lorentz transformation would shift this pseudo-current density into a pseudo-charge density.  This does not happen however, because the vector identity involving the divergence of a curl still applies.  The Aharonov-Bohm phenomenon, first viewed as a purely quantum effect, may have a classical analogue in the unified field equations.  

The field equations involving the gravitational force field are dynamic and depend on four dimensions.  This makes them likely to be consistent with special relativity.  Since they are generated alongside the Maxwell equations, one can reasonably expect the differential equations will share many properties, with the ones involving the symmetric-matrix gravitational force field being more symmetric than those of the electromagnetic counterpart.  

The unified source can be defined in terms of more familiar charge and current densities by separately setting the gravity or electromagnetic field equal to zero.  In these cases, the source is due only to electricity or mass respectively.  This leads to connections between the unified source, mass, and charge:

It would be incorrect - but almost true - to say that the unified charge and current are simply the sum of the three: mass, electric charge, and the Aharanov-Bohm pseudo-current (or total magnetic flux over the volume).  These terms constructively interfere with each other, so they may not be viewed as being linearly independent.

Up to four linearly independent unified field equations can be formulated.  A different set could be created by using the differential operator without taking its conjugate:

This is an elliptic equation.  Since the goal of this work is a complete system of field equations, this may turn out to be an advantage.  An elliptic equation combined with a hyperbolic one might more fully describe gravitational and electromagnetic waves from sources.  Unlike the first set of field equations, the cross terms destructively interfere with each other.

The elliptic field equation again contains three of four Maxwell equations explicitly:Gauss' law, the no magnetic monopoles vector identity and Faraday's law.  This time, Ampere's law looks different.  To be consistent with Ampere's law, again a pseudo-current must be included.  This may be the differential form of a classical Aharonov-Bohm effect.  

The only term that does not change between the two field equations is the one involving the dynamic gravitational force.  This might be a clue for why this force is only attractive.

All the solutions that have been worked out for the Maxwell equations will work with the unified field equations.  For example, if the potential is static, the scalar equation for hyperbolic field equation is the Poisson equation.  The unified equations are more informative, since any potential which is a solution to the scalar Poisson equation will also characterize the corresponding current.  

The field equations of general relativity and the Maxwell equations both have vacuum solutions,such as plane wave solutions. The unified field equations do not have such a solution, other than a constant.  Given historical tradition, this may seem like a deadly flaw.  However, it may be something that is required for a final and complete theory.  In a unified field theory, the gravitational part may be zero while the electrical part is not, and visa versa.  Non-zero solutions are worth exploring

.An inverse square potential plays an important role in both gravity and electromagnetism. Examine the scalar field involving the inverse interval squared:

This potential solves the Maxwell equations in the Lorentz gauge:

The non-zero part may have everything to do with gravity.

A plane wave solution does exist,but not for a pure vacuum.Instead,a plane wave solution exists with the constrain that the net current is zero for the elliptical field equations

The field equations of general relativity and the Maxwell equations both have vacuum solutions.  A vacuum solution for the unified field equation is apparent for the elliptical field equations:

The unified field equation will evaluate to zero if

The dispersion relation is an inverted distance, so it will depend on the metric.  The same potential can also solve the hyperbolic field equations under different constraints and resulting dispersion equation (not shown).  There were two reasons for not including the customary imaginary number "i" in the exponential of the potential.  First, it was not necessary.  Second, it would have created a complex-valued quaternion, and therefore is outside the domain of this paper.  The important thing to realize is that vacuum solutions to the unified field equations exist whose dispersion equations depend on the metric.  This is an indication that unifying gravity and electromagnetism is an appropriate goal.

Conservation of electric charge is implicit in the Maxwell equations.  Is there also a conserved quantity for the gravitational field? Examine how the differential operator acts on the unified field equation:

Notice that the gravitational force field only appears in the quaternion scalar.  The electromagnetic fields only appear in the 3-vector.  This generates two types of constraints on the sources.  No change in the electric source applies to the quaternion scalar.  No change in the gravitational source applies to the 3-vector.

The first equation is known as the continuity equation, and is the reason that electric charge is conserved.  For a different inertial observer, this will appear as a conservation of electric current density.  There is no source term for the Aharanov-Bohm current, and subsequently no conservation law.  The 3-vector equation is a constraint on the mass current density, and is the reason mass current density is conserved.  For a different inertial observer, the mass density is conserved.

The transformation properties of the unified field promise to be more intricate than either gravity or electromagnetism separately.  What might be expected to happen under a Lorentz transformation? Gravity involves mass that is Lorentz invariant, so the field that generates it should be Lorentz invariant.  The electromagnetic field is Lorentz covariant.  However, a transformation cannot do both perfectly.  The reason is that a Lorentz transformation mixes a quaternion scalar with a 3-vector.  If a transformation left the quaternion scalar invariant and the 3-vector covariant, the two would effectively not mix.  The effect of unification must be subtle, since the transformation properties are well known experimentally.

Consider a boost along the x-axis.  The gravitational force field is Lorentz invariant.  All the terms required to make the electromagnetic field covariant under a Lorentz transformation are present, but covariance of the electromagnetic fields requires the following residual terms:

At this time, the correct interpretation of the residual term is unclear.  Most importantly, it was shown earlier that charge is conserved.  These terms could be a velocity-dependent phase factor.  If so, it might provide a test for the theory.

The mechanics of the Lorentz transformation itself might require careful re-examination when so strictly confined to quaternion algebra.  For a boost along the x-axis, if only the differential transformation is in the opposite direction, then the electromagnetic field is Lorentz covariant with the residual term residing with the gravitational field.  The meaning of this observation is even less clear.  Only relatively recently has DeLeo been able to represent the Lorentz group using real quaternions (S. De Leo, "Quaternions and special relativity," J. Math. Phys., 37(6):2955-2968, 1996).  The delay appears odd since the interval of special relativity is the scalar of the square of the difference between two events.  In the real 4x4 matrix representation, the interval is a quarter of the trace of the square.  Therefore, any matrix with a trace of one that does not distort the length of the scalar and 3-vector can multiply a quaternion without effecting the interval.  One such class is 3-dimensional, spatial rotations.  An operator that adds nothing to the trace but distorts the lengths of the scalar and 3-vector with the constraint that the difference in lengths is constant will also suffice.  These are boosts in an inertial reference frame.  Boosts plus rotations form the Lorentz group.

Three types of gauge transformations will be investigated: a scalar, a 3-vector, and a quaternion gauge field.  Consider an arbitrary scalar field transformation of the potential:

The electromagnetic fields are invariant under this transformation.  An additional constraint on the gauge field is required to leave the gravitational force field invariant, namely that the scalar gauge field solves a homogeneous elliptical equation.  From the perspective of this proposal, the freedom to choose a scalar gauge field for the Maxwell equations is due to the omission of the gravitational force field.

Transform the potential with an arbitrary 3-vector field:

This time the gravitational force field is invariant under a 3-vector gauge field transformation.  Additional constraints can be placed on the 3-vector gauge field to preserve a chosen electromagnetic invariant.  For example, if the difference between the two electromagnetic fields is to remain invariant, then the 3-vector gauge field must be the solution to an elliptical equation.  Other classes of invariants could be examined.

The scalar and 3-vector gauge fields could be combined to form a quaternion gauge field.  This gauge transformation would have the same constraints as those above to leave the fields invariant.  Is there any such gauge field? The quaternion gauge field can be represented the following way:

If a force field is created by hitting this gauge transformation with a differential operator, then the gauge field becomes a unified field equation.  Since vacuum solutions have been found for those equations, a quaternion gauge transformation can leave the field invariant.

The fields of gravity and electromagnetism were unified in a way consistent with Einstein's vision, not his technique.  The guiding principles were simple but unusual:generate expressions familiar from electromagnetism using quaternions, striving to interpret any extra terms as being due to gravity.  The first hypothesis about the unified field involved only a quaternion differential operator acting on a potential, no extra terms added by hand.  It contained the typical potential representation of the electromagnetic field, along with a symmetric-matrix force field for gravity.  The second hypothesis concerned a unified field equation formed by acting on the unified field with one more differential operator.  All the Maxwell equations are included explicitly or implicitly.  Additional terms suggested the inclusion of a classical representation of the Aharanov-Bohm effect.  Four linearly independent unified field equations exist, but only the hyperbolic and elliptic cases were discussed.  A large family of vacuum solutions exists, and will require future analysis to appreciate.  To work within the guidelines of this paper, one should avoid solutions represented by complex-valued quaternions.  

Why did this approach work? The hypothesis that initiated this line of research was that all events in spacetime could be represented by quaternions, no matter how the events were generated.  This is a broad hypothesis, attempting to reach all areas covered by physics.  Based on the equations presented in this paper, a logical structure can be constructed, starting from events (see Fig. 2). A set of events forms a pattern that can be described by a potential. The change in a potential creates a field. The change in field creates a field equation.  The terms that do not change under differentiation of a field equation form conservation laws.  

Acknowledgements

Thanks for many productive discussions Prof.Guido Sandri.