A Critique of the Maxwell Equations
Maxwell's Explicit Vision
Simple Equations with Simple Solutions
The 3 Fields: g, E & B
Field Equations: ~Maxwell and a Dynamic g
Recreating Maxwell
Unified Field Equations
Conservation Laws
Gauge Transformations
Equations of Motion
Unified Equations of Motion
Missing Links

Einstein devoted the last half of his life to trying to unify gravity and electromagnetism.  While he did not succeed, the reasoning was clear:

The physical world is represented as a four-dimensional continuum.  If in this I adopt a Riemannian metric, and look for the simplest laws which such a metric can satisfy, I arrive at the relativistic gravitation theory of empty space.  If I adopt in this space a vector field, or the antisymmetric tensor field derived from it, and if I look for the simplest laws which such a field can satisfy, I arrive at the Maxwell equations for free space...at any given moment, out of all conceivable constructions, a single one has always proved itself absolutely superior to all the rest...

There are four elements vying for attention: symmetry and simplicity, consistency and completeness.  In the analysis below, I will come back to one of these four horsemen to move the line of logic forward.

There are four equations that compose the set referred to as the Maxwell equations.  What are the appropriate signs for these terms?  Maxwell inherited from experimentalists four equations.  All the divergences and curls were positive.  Only for one of them (Ampere's law) did he add a term, whose sign was chosen so that the equation was hyperbolic (a wave propagating from a surface).  For the no monopole equation, the sign of the divergence of the magnetic field does not have any information.  However, when bundled together in a second-rank tensor, the signs of terms relative to each other matters.  Here are the four equations (Gauss, Faraday, Ampere, and no monopoles respectively):

The del vector operator, acting on E or B as a curl or a divergence, generates a positive sign.  The scalar time derivative flips signs between E and B.

Consider what it takes to form these six terms with a simple quaternion expression:

The divergence always necessarily has a sign which is opposite to the curl.  If the divergences of the vectors have the same sign, and the curls of the vectors have the same signs, then the time derivatives should have the same signs.  To be simple and consistent, the signs of three of terms that form the Maxwell equations need to be changed.  However, changing the signs of terms changes their meaning.  Simple quaternion equations with unfamiliar collections of signs will be examined closely to see is the standard structure is there, along with a few surprises.

Notice how the scalar is zero.  This indicates that the Maxwell equations are not complete, that an obvious opportunity to store information about nature is ignored when the generator of the terms in the Maxwell equations is expressed with quaternions.

In Maxwell's "Treatise on Electricity and Magnetism", he expressed the hope that electromagnetism could be represented with quaternions someday.  That hope has been realized in an earlier section (Classical Electromagnetism).  That required the use of operators: commutators, anticommutators, and one that isolates the vector.  If that expression is written only in terms of the potential and the differential, it requires 56 terms!

This is not simple.  Given a source, it would be very difficult if not impossible to determine what potential created it.

Starting from a potential, the Maxwell equations are a second order differential equation.  It has been shown just how complicate the generators of the terms are.  What would the simplest quaternion second order differential equation be?

Given a source, finding the potential would involve acting on this equation on the left with two inverse differential operators:

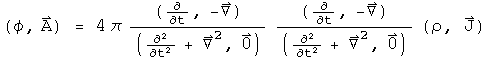
The signs on the generator equation happened to be all positive.  There are 2^6 = 64 different choices for the signs of the simplest generator of a second order quaternion differential equation.  Although one could write out all 64 possibilities (and I have :-), there are only two independent second order differential equations.  The 9 patterns of terms that emerge from the ensemble of 64 can be interconverted by exchanging -phi for phi, -A for A, mirror symmetry operations, or combinations of these.  Not a single one of them has the signs that appear with the Maxwell equations.  The sign of the divergence is always opposite to the sign of the curl.

The electric and magnetic field can be represented by potentials.  The terms can be generated by a first order differential equation.  I will use a sign convention used by Feynman.

Look at the connection between the field definition and its matrix representation

If the order of the differential operator and the potential were reversed, only the term with the cross product would change signs. That is what determines if a term is even or odd.  In the matrix representation of a quaternion, the scalar forms the diagonal, so transposing the matrix leaves the diagonal unchanged, so it is symmetric.  The 3-vector terms are antisymmetric because transposing the matrix flips the signs.

Gravity is the result of a metric, a symmetric tensor.  Electromagnetism involves an antisymmetric tensor.  At least on the surface, it appears like these field have the correct symmetries for unifying gravity and electromagnetism as foreseen by Einstein.

Field equations are formed by acting on the fields with the differential operator.

This generates 6 field equations.

These are not the standard Maxwell equations, although every term in those equations is represented.  The two scalar equations flip signs.  That has no impact on the physics, just sign conventions.  Ben Franklin would be happy :-)

Maxwell included a current for Ampere's law, and chose the sign of that term, possibly to make charge conservation apparent (that will be done later).  The relative sign also makes the equations have hyperbolic solutions, appropriate for propagating waves.  This proposal involves elliptic equations.  An electromagnetic wave and its matter source must be thought of together inside a surface.  This surface can change (at the speed of light I suspect!).  This has possibly interesting implications in cosmology, with all the activity of the Universe confined to be inside the expanding surface of the Big Bang.

The scalar force field is dynamic rather than a static component as is the case for Newton's law.  There are also tidal effects that must be accounted for.  g has a dynamic equation and a gradient, so these field equations have the structure to do both.  This proposal stands a better chance of being compatible with special relativity that Newton's law.

Another linearly independent second order differential equation can be formed using a conjugate differential operator.

This generates 6 more slightly different field equations.

This appears to be closer the Maxwell equations, but still fundamentally different.  As before, all terms are included.  Gauss' law and the divergence of B are standard.  Ampere's law appears with a sign change.  This is a hyperbolic wave equation.  The problem here is that Faraday's law is no longer an identity.

Notice that the only equation that does not change in going from elliptical to hyperbolic equations is the one involving dynamic g.  This might be a reason why gravity is unidirectional.  Or maybe not :-)

Since we have two equations, one elliptic, the other hyperbolic, that contain all the terms of the Maxwell equations, it would be a shame not to recreate the explicit form of the Maxwell equations, given their enormous success.  This can be done with smoke and mirrors, or more precisely, a linear combination of the two equations, conjugates, and one mirror operation.

Consider the sum and the difference:

The sum generates only time derivatives.  The difference isolates spatial derivatives, the divergences and curls.  If a mirror transformation is done on the sum, the 3-vector E will change signs, but the psuedovector B will not.  The scalar is unchanged.  Combine these results.

The Maxwell equations are not a simple linear combination of the two quaternion differential equations.  Conjugates and a mirror operation are required to get them in their proper form.  

This is the sum of the Maxwell equations.  Can individual equations be generated?  With all these equations and mirrors, anything is possible :-)

The homogeneous Maxwell equations can be isolated completely separated from terms involving the field g, but the source equations are linked.

Although equations for electricity and (possible) gravity are appearing in the same quaternion equation, they are not really unified.  The generator for the field equation will be written from potentials.  This will lead to additional cancellations that create a real unification.

One reason for the unification of electricity and magnetism can be seen by the complete cancellation of terms under the name of Faraday's law.  There are two other cancellations occurring, but they are not complete, between g and E.  One happens with the scalar terms, the other with the vector terms.  It appears reasonable to state that the only way to get a partial cancellation is if the two fields are unified.  The magnetic field is not a direct participant.

Examine the hyperbolic equation written in potential form.

This time, parts of the fields g and E add, as do E and B to make the extra curl of A dot term.  The hyperbolic equation includes two vector identities.

Recreating the Maxwell equations, this time from potentials:

This looks similar to the Maxwell equations written in the Lorenz gauge, but there are two additional vector identities and terms for gravity.

Act on the field equations with a differential:

Algebraically, this is similar to the unified field equations, where the two differential operators acted on the potential instead of the fields.  There are two conservation laws here created by cancellations, charge conservation for electromagnetism in the scalar, and a vector conservation for gravity.

In the classical region, Newton's force is the gradient of a static potential.  The force is conservative, and this vector conservation law is consistent with that.  In the relativistic region, there is no force field, everything cancels.  All that remains is a simple scalar second order differential equation.  That was one of the central messages of general relativity: gravity is not a force, it is curvature.  Everything about g is described by an scalar elliptic equation.

If the differential operator acts on the hyperbolic equation,  analogous results are obtained:

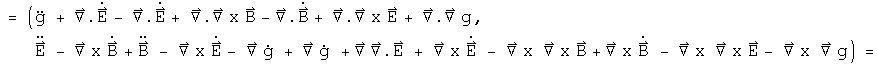
There are two conservation laws here, charge conservation for electromagnetism in the scalar, and a vector conservation for gravity.

The hyperbolic equations have a charge conservation law consistent with the Maxwell equations.  It must be consistent with the standard conservation of charge, since the Maxwell equations can be written as a combination of the elliptic and hyperbolic quaternion equations.

Three types of gauge transformations will be considered: with an arbitrary scalar field, an arbitrary 3-vector field, and a quaternion field.  It will be shown that unification of gravity and electromagnetism adds an additional constraint to these types of transformations.

First, let lambda be an arbitrary scalar field.  Consider this transformation of the potential:

See how this changes the fields:

Just like the Maxwell equations, an arbitrary scalar field does not effect the vector fields E and B.  However, there is an additional scalar field g which requires an additional constraint to remain invariant, namely that the scalar gauge field lambda solves a homogeneous elliptical equation.  The gauge freedom seen in the Maxwell equations is due to their incompleteness.

Let capital Lambda be an arbitrary vector field.  Transform the potential like so:

Examine the effects on fields:

This time the scalar field g is invariant under a vector gauge field transformation.  Additional constraints are placed on the gauge field by E and B.  I choose to detail one form that left the difference between the E and B fields invariant.  There are many more constraints that could be examined.

The scalar and vector gauge fields could be combined to form a quaternion gauge field.  This gauge transformation would have the same constraints as those above to leave the fields invariant.  A big question is why there are any such gauge fields.  The reason is simple: because there are homogeneous solutions to the second order differential quaternion equations.  The quaternion gauge field can be represented the following way:

The fields are formed by acting on this with a differential operator.  The field equations are second order equations, as are those terms involving lambda.  If these second order terms are part of a homogeneous solution, the fields will be invariant under the gauge transformation.

Equations of motion are generated just like the field equations, except that the 4-velocity is used instead of the differential operator:

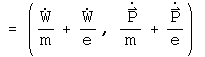
There are two equations for work, two equations for momentum, and two identities.

This is, admittedly, an unorthodox approach to defining a force.  It was noticed that this operation on a field generated precisely the Lorentz force, and had a term for the energy of the E field up to a sign.  There are no miracles in math.  For the sake of completeness, the other terms should also have a meaning.  Terms analogous to the homogeneous Maxwell equations become homogeneous force equations.

The energy equation has aa sign opposite of the convention, which is consistent with other changes proposed in this section.  The identities in the table are usually not discussed.  Think about the differential operator and the 4-velocity.

The direction of the 3-vector in both terms is identical, so any identity involving the 3-vector field equations will apply to 3-vector forces.

It is absolutely essential that Newton's law can explicitly be found here.  There will have to be a lot of thinking about signs here, but the form is correct.  Newton's law by itself is not consistent with special relativity.  Fortunately, there is another term.

This looks like it should get along with special relativity just fine!

Repeat the exercise from above, but this time, look to the potentials.

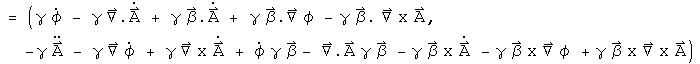
That is pretty complicated!  The key to simplifying this equation is to see what happens for light, where dt/dx = dx/dt.  Gamma blows up, but if the equation is over gamma, that problem becomes a scaling factor.  With beta equal to one, a number of terms cancel, which can be seen more clearly if the terms are written out explicitly.

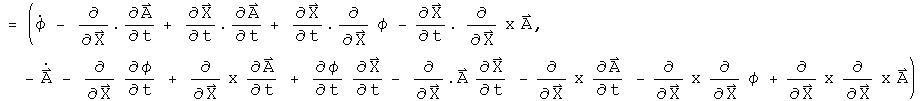
It would take a real mathematician to state the proper constraints on the three pairs of cancellations that happen when velocities get flipped.  There are also a pair of vector identities, presuming simple connectedness.  This leads to the following equation:

The scalar change in energy depends only on the scalar potential, and the 3-vector change in momentum only depends on the 3-vector A.

Quaternions have 4 degrees of freedom, yet I have analyzed only two types of second order differential equations.  This may be due to the current limitations of quaternion analysis, a topic I have been making much progress on of late.  My sense it that once the quaternion derivative is well defined (and I am working on a strong candidate), it will be clear how to proceed.  My dream is that spinors will magically appear :-)

Note added later: Work with the first and second conjugates does look like it is involved with spin.  Wherever there is a conjugate, swapping in the first or second conjugate will form a linearly independent differential equation.  Now four sets of equations can be written, but what it all means is still a mystery :-)

Take Newton's law, make it relativistic, and general relativity is the result.  General relativity has passed a number of experimental tests.  It looks like this unified field theory may make similar, if not identical predictions.  At this point, I have not been able to do those calculations.  The prediction of this theory for the experimental tests of general relativity must be developed.  Until then...