Abstract
Introduction
Relativistic 4-forces
The constant velocity profile solution
Future directions

In quantum electrodynamics, photons have four modes of transmission, at least mathematically: two transverse modes for electrodynamics, a longitudinal, and a scalar mode. The probabilities of the last two modes cancel each other out for photons in a vacuum, but that does not have to be the case for a nonhomogeneous equation. One potential solution to the field equations is found which depend on the inverse of an interval between two events squared. The force field created by the potential is constructed by comparison with the classical Newtonian gravitational field. The Lagrange density L= scalar(-(J A*) - 1/2 Box* A Box A*) can contribute to a scalar mode, but still has the field equations of Maxwell with the choice of the Lorenz gauge. A relativistic force equation is proposed, created by the product of charge, normalized force field, and 4-velocity: dmU/dtau = kq Box* A/|A| U*. The solution to the force equation using the inverse square interval potential is found. Eliminating the constants generates a metric equation, (dtau)^2 = e^-(2GM/c^2 tau) dt^2 - e^(2GM/c^2 tau) dR^2, where tau  is a lightlike interval with almost the same magnitude as the radius R of separation between source and test masses. For a weak gravitational field, the metric will pass the same tests as the Schwarzschild metric of general relativity. The two metrics differ for higher order terms, which makes the proposed metric distinct and testable experimentally. A constant-velocity solution exists for the gravitational force equation for a system with an exponentially-decaying mass distribution. The dark matter hypothesis is not needed to explain the constant-velocity profiles seen for some galaxies. Gravity is a metric theory, electromagnetism is not.  By using Riemannian quaternions which can have dynamic basis vectors, it becomes possible to merge metric theory with the linear Maxwell equations.  The proposal may also have implications for classical big bang theory.

The electrodynamic field can be quantized in a manifestly covariant form by fixing the gauge (K. Bleuler, Helv. Phys. Acta, 23:567, 1950, and S. N. Gupta, "Theory of longitudinal photons in quantum electrodynamics", Proc. Phys. Soc., 63:681-691). The starting point is the 4-potential A^mu. There are four modes of transmission for photons corresponding to the four degrees of freedom: two transverse, one scalar, and one longitudinal. Gupta calculated that "the probability of the emission of a real longitudinal photon is canceled by the 'negative probability' of the emission of a corresponding scalar photon." He notes that this does not always have to be the case for the nonhomogeneous Maxwell equations, which is the focus of this work. A scalar photon would not change signs under a space or time reversal, so its symmetry is different from the electric 3-vector field and the magnetic 3-pseudo-vector field, and thus does not have an obvious role to play in electrodynamics.

My hypothesis is that the scalar and longitudinal photons for the electromagnetic field constitute gravity. The hypothesis makes several predictions even at this preliminary stage. First, the math of gravity and electromagnetism should be similar but not identical. The inverse square form of Newton's law of gravity was a direct inspiration for Coulomb's law. Gravity should be more symmetric than electromagnetism because the mode is scalar, instead of transverse. The second rank field strength tensor in general relativity is symmetric while the analogous tensor for the electromagnetic field is antisymmetric. Since the mode of gravity is orthogonal to electromagnetism, the charges can be likewise, so there will be no simple relationship between gravitational charge (mass) and electric charge. Gravitational waves in general relativity are transverse, so this proposal is distinct from general relativity. Nature exploits all the math available, so it is unreasonable to suppose that scalar and longitudinal photons are never used for anything. Whatever phenomenon exploits the scalar and longitudinal photons must be similar, but just as important as electromagnetism. Gravity is a natural candidate.

A gravitational field inside Maxwell

Newton's classical gravitational law arises from a scalar potential.Here is the scalar field equation:

For the case of a vacuum, when rho = 0, this is known as the Laplace equation. For a spherically symmetric source, one solution is:

The problem with the field equation is that the Laplace operator does not have a time differential operator. Any change in in the mass density propagates at infinite speed, in conflict with special relativity (MTW, chapter 7).  One way to derive the field equations of general relativity involves making Newton's law of gravity consistent with the finite speed of light.

A way to repair the field equations is to use the D'Alembertian operator, which is four dimensional. That expression is identical to the A^0 component of the Maxwell equations with the choice of the Lorenz gauge.  The sources are of course different.  Yet the argument being made here is that there are degrees of freedom which have yet to be exploited.  For the two degrees of freedom, we can have a different source term, mass:

If one is studying scalar or longitudinal modes, the source is J_mass, the mass current density.  If one is working with transverse modes, the source is J_charge^mu , the electric charge density. Since the modes are orthogonal, the sources can be also.

To be consistent with the classic scalar potential yet still be relativistic, the potential must have x^2, y^2, z^2, and t^2. This suggests a particular solution to the field equations:

This potential is interesting for several reasons. It is the inverse of the Lorentz-invariant interval squared. Like mass, the 4-potential will not be altered by a change in an inertial reference frame. The interval between any two events will contribute to the potential. General relativity applies to any form of energy, including gravitational field energy. A potential that embraces every interval may have a broad enough scope to do the work of gravity.

The potential also has serious problems. Classical gravity depends on an inverse square force field, not an inverse square potential. Taking the derivative of the potential puts a forth power of the interval in the denominator. At this point, I could stop and say that this potential has nothing to do with gravity because it has the wrong dependence on distance. An alternative is to look for an algebraic way to repair the problem. This is the type of approach used by the early workers in quantum mechanics like de Broglie, and will be adopted here. The equations of motion can be normalized to the magnitude of the 4-potential:

Since the magnitude of the potential is the inverse interval squared, the resulting equation has only an interval squared in the denominator. An interval is not necessarily the same as the distance R between the source and test mass used in the classical theory. However, I can impose a selection rule that in the classical limit, the only events that contribute to the potential are those that are timelike separated between the source and the test masses. It takes a timelike interval to know that the source is a distance R away. Action-at-a-distance respects the speed of light as it must.

Search for the source mass

Where is the source mass in the potential? All that has been discussed so far is an interval, a distance, nothing about mass. An idea from general relativity will be borrowed, that mass can be treated geometrically if multiplied by the constants G/c^2. The distance between the Earth and the Sun is approximately 1.5x10^11 m, while the Sun's mass expressed in units of distance, GM_Sun/c^2, is 1.5x10^3 m, eight orders of magnitude smaller. The overall length of the interval will not be changed noticeably if the spatial separation and the Sun's mass expressed as a distance are summed. However, the force field is the derivative of the potential, and any change in position in spacetime will have a far greater effect proportionally on the smaller geometric mass than the spatial separation. Make the following change of variables:

where A and B are locally constants such that tau^2 ~= A^2 - B^2. The change of variables is valid locally, but not globally, since it breaks down for arbitrarily long time or distance away.  General relativity is also valid locally, not globally.

What is the physical interpretation of the inverse square potential and the above substitution? Newton observed that motion in an ellipse could be caused by either a linear central force or an inverse square law.  With the above substitution, there is a linear displacement equation inside an infusers square potential. It is like a simple harmonic oscillator inside a simple harmonic oscillator! This oscillator works with four dimensions. Although it is confusing to confront the idea of oscillations in time, there is no need worry about it, since the equations are quite simple and their mathematical consequences can be worked out.   If all the terms where included, the equation would be nonlinear.

The field is the derivative of the potential.  To be correct technically, it is the contravariant derivative.  This requires both a metric and a connection.  In effect, all the work presented with quaternions uses the Minkowski metric with Cartesian coordinates.  For such a choice of metric and coordinates, the contravariant derivative equals the normal derivative.  The derivative of the potential under study, a normalized interval squared with the linear displacement substitution, is approximately:

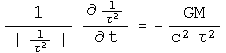
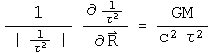
This should look familiar, remembering that employing the event selection rule from above, the magnitude of tau ^2 is almost the same as R^2, differing only by the geometric mass of the source.

Despite its formulation using quaternions, this unification proposal is strikingly similar to earlier work.  Gupta wanted to quantize the radiation field using a form that was manifestly covariant in its explicit treatment of time and space. He fixed the gauge with this Lagrange density:

The equations of motion for this Lagrangian are the same as choosing the Lorenz gauge:

The problem with the Lagrangian is that the field strength tensor is antisymmetric. Due to the zeros along the diagonal, it cannot contribute directly to a scalar mode. What is needed is a Lagrange density that could contribute directly to the scalar mode but still have the same field equations. Here is such a Lagrangian:

This is not as miraculous as it might first appear. It is the first of four terms generated in the contraction of the electromagnetic field strength tensor. In essence, information is not discarded, which is what happens in making the field strength tensor antisymmetric.

A relativistic 4-force is the change in momentum with respect to the interval. The covariant force law is similar in form to the one for electromagnetism except that the second rank tensor is asymmetric and normalized:

If this equation is to transform like the Lorentz 4-force of electromagnetism, the normalized potential must be invariant under a Lorentz transformation.  That is the case of the potential under study.

In the first application of the force law, assume the derivative of the mass with respect to the interval is zero. For the scalar photons, assume the charge q is the gravitational test mass. Experiments have demonstrated that gravitational and inertial masses are equal. Assuming spherical symmetry, the inverse interval squared potential leads to the following equations of motion:

Solve these second-order differential equations for the spacetime position:

where Ei is the exponential integral, Ei(t)=the integral from negative infinity to t of e^t/t dt.  The exponential integral plays other roles in quantum mechanics, so its presence is interesting.  

Eight constants need to be eliminated:(c_1, C_1) and (c_2, C_2).  Take the derivative of the spacetime position with respect to tau.  This eliminates four constants, (c_2, C_2).  The result is a 4-velocity:

In flat spacetime, beta _mu beta^mu=1, providing four more constraints.  Spacetime is flat if M goes to 0 or tau goes to infinity, leading to e^(GM/c^2|tau |) goes to 1:  

Solve for c_1^2 and C_1.C_1:

Substitute back into the flat spacetime constraint.  Rearrange into a metric:

If the gravitational field is zero, this generates the Minkowski metric of flat spacetime.  Conversely, if the gravitational field is non-zero, spacetime is curved

As expected, this become the Minkowski metric for flat spacetime if M goes to 0 or tau goes to infinity.

No formal connection between this proposal and curvature has been established.  Instead a path between a proposed gravitational force equation and a metric function was sketched.  There is a historical precedence for the line of logic followed.  Sir Isaac Newton in the Principia showed an important link between forces linear in position and inverse square force laws.  More modern efforts have shown that the reason for the connection is due to the conformal mapping of z goes to z^2 (T. Needham, "Newton and the transmutation of force," Amer. Math. Mon., 100:119-137, 1993).  This method was adapted to a quaternion force law linear in the relativistic velocity to generate a metric.  

For a weak field, write the Taylor series expansion in terms of the total mass over the interval to second-order in M/|tau|:

Contrast this with the Schwarzschild solution in isotropic coordinates expanded to second order in M/R (MTW, eq. 31.22):

The magnitude of the lightlike interval tau in the unified field metric is nearly identical to the radius R in the Schwarzschild metric, the difference being the geometric mass of the source included in the interval \tau . The metric for the scalar potential will pass the same weak field tests of general relativity as the Schwarzschild metric to post-Newtonian accuracy, which does not use the second order spatial term. The difference in the higher order terms can be the basis of an experimental test to distinguish this proposal from general relativity. Since the effect is second order in the field strength, such a test will challenge experimental techniques.

The two metrics are numerically very similar for weak fields, but mathematically distinct.  For example, the Schwarzschild metric is static, but the unified metric contains a dependence on time so is dynamic.  The Schwarzschild metric has a singularity at R=0.  The unified gravitational force metric becomes undefined for lightlike intervals.  This might pose less of a conceptual problem, since light has no rest mass.  

In the previous section, the system had a constant point-source mass with a velocity profile that decayed with distance.  Here the opposite situation is examined, where the velocity profile is a constant, but the mass distribution decays with distance.  Expand the definition of the relativistic force using the chain rule:

The first term of the force is the one that leads to an approximation of the Schwarzschild metric, and by extension, Newton's law of gravity.  For a region of spacetime where the velocity is constant, this term is zero.  In that region, gravity's effect is on the distribution of mass over spacetime.  This new gravitational term is not due to the unified field proposal per se.  It is more in keeping with the principles underlying relativity, looking for changes in all components, in this case mass distribution with respect to spacetime.

Start with the gravitational force in a region of spacetime with no velocity change:

Make the same assumptions as before: the gravitational mass is equal to the inertial mass and the gravitational field employs the interval between the worldlines of the test and gravitational masses.  This generates an equation for the distribution of mass:

Solve for the mass flow:

As in the previous example for a classical weak field, assume the magnitude of the interval is an excellent approximation to the radius divided by the speed of light.  The velocity is a constant, so it is the mass distribution that shows an exponential decay with respect to the interval, which is numerically no different from the radius over the speed of light.  This is a stable solution.  If the mass keeps dropping of exponentially, the velocity profile will remain constant

Look at the problem in reverse.  The distribution of matter has an exponential decay with distance from the center.  It must solve a differential equation with the velocity constant over that region of spacetime like the one proposed.

The exponential decay of the mass of a disk galaxy is only one solution to this expanded gravitational force equation.  The behavior of larger systems, such as gravitational lensing caused by clusters, cannot be explained by the Newtonian term (A. G. Bergmann, V. Petrosian, and R. Lynds, "Gravitational lens images of arcs in clusters," Astrophys. J., 350:23, 1990. S. A. Grossman and R. Narayan, "Gravitationally lensed images in abell 370," Astrophys. J., 344-637-644, 1989. J. A. Tyson, F. Valdes, and R. A. Wenk, "Detection of systematic gravitational lens galaxy image alignments: Mapping dark matter in galaxy clusters," Astrophys. J. Let., 349:L1, 1990).  It will remain to be seen if this proposal is sufficient to work on that scale.

Gravity was first described as a force by Isaac Newton.  In general relativity, Albert Einstein argued that gravity was not a force at all.  Rather, gravity was Riemannian geometry, curvature of spacetime caused by the presence of a mass-energy density.  Electromagnetism was first described as a force, modeled on gravity.  That remains a valid choice today.  However, electromagnetism cannot be depicted in purely geometric terms.  A conceptual gap exists between purely geometrical and force laws.  

The general equivalence principle, introduced in the first paper of this series, places geometry and force potentials on equal footing.  Riemannian quaternions, (a_0 i_0,a_1 i_1/3,a_2 i_2/3,a_3 i_3/3), has pairs of (possibly) dynamic terms for the 4-potential A and the 4-basis I.  Gauss' law written with Riemannian quaternion potentials and operators leads to this expression:

If the divergence of the electric field E was zero, then Gauss' law would be due entirely to the divergence of the basis vectors.  The reverse case could also hold.  Any law of electrodynamics written with Riemannian quaternions is a combination of changes in potentials and/or basis vectors.

An algebraic path between a solution to the Maxwell equations and a classical metric gravitational theory has been shown. No effort has been extended yet to quantize the unification proposal. Like the early work in quantum mechanics, a collection of hunches is used to connect equations. One is left with the question of why this might work? The action of a gauge invariant theory cannot be inverted to generate the propagator needed for quantum mechanics. Fixing the gauge makes the action invertible, but the additional constraint decreases the degrees of freedom. By using quaternions, a division algebra, the equation is necessarily invertible without imposing a constraint. If the operation of multiplication surpasses what can be done with division, then Nature cannot harness the most robust mathematical structure, a topological algebraic field, the foundation for doing calculus. Nature does calculus in four dimensions, and it is this requirement that fixes the gauge. In the future, when we understand how to do calculus with four-dimensional automorphic functions, we may have a deep appreciation of Nature's methods.

There is a physical explanation for gravity - it is a local, nonlinear, four-dimensional simple harmonic oscillator.  Gravity is all about oscillations.  The Earth returns to approximately the same place after one year of travel.  If there were no interfering matter in the way, an apple dropped would fall to the center of the Earth, reach the other side, and return in a little over eighty minutes.  The metric equation that results from this analysis is within the experimental constraints of current tests of general relativity.  That makes the proposal reasonable.  For higher order terms of a weak field, the proposal is different than the Schwarzschild metric of general relativity.  That makes it testable.  There are very few reasonable, testable classical unified field theories in physics, so this alone should spark interest in this line of work.

For a spiral galaxy with an exponential mass distribution, dark matter is no longer needed to explain the flat velocity profile observed or the long term stability of the disk.  Mass distributed over large distances of space has an effect on the mass distribution itself.  This raises an interesting question: is there also an effect of mass distributed over large amounts of time? If the answer is yes, then this might solve two analogous riddles involving large time scales, flat velocity profiles and the stability of solutions.  Classical big bang cosmology theory spans the largest time frame possible and faces two such issues.  The horizon problem involves the extremely consistent velocity profile across parts of the Universe that are not casually linked (MTW, p. 815).  The flatness problem indicates how unstable the classical big bang theory is, requiring exceptional fine tuning to avoid collapse.  Considerable effort will be required to substantiate this tenuous hypothesis.  Any insight into the origin of the unified engine driving the Universe of gravity and light is worthwhile.