Rotations + dilations
Implications

In 1905, Einstein proposed the principles of special relativity without a deep knowledge of the mathematical structure behind the work.  He had to rely on his old math teacher Minkowski to learn the theory of transformations (I do not know the details of Einstein's education, but it could make an interesting discussion :-)  Eventually, Einstein understood general transformations, embodied in the work of Riemann, well enough to formulate general relativity.

A. W. Conway and L. Silberstein proposed a different mathematical structure behind special relativity in 1911 and 1912 respectively (a copy of Silberstein's work is on the web.  Henry Baker has made it available at ftp://ftp.netcom.com/pub/hb/hbaker/quaternions/).  Cayley had observed back in 1854 that rotations in 3D could be achieved using a pair of quaternions with a norm of one:

If this works in 3D space, why not do the 4D transformations of special relativity?  It turns out that a and b must be complex-valued quaternions, or biquaternions.  Is this so bad?  Let me quote P.A.M. Dirac (Proc. Royal Irish Academy A, 1945, 50, p. 261):

Quaternions themselves occupy a unique place in mathematics in that they are the most general quantities that satisfy the division axiom--that the product of two factors cannot vanish without either factor vanishing.  Biquaternions do not satisfy this axiom, and do not have any fundamental property which distinguishes them from other hyper-complex numbers.  Also, they have eight components, which is rather too many for a simple scheme for describing quantities in space-time.

Just for the record: plenty of fine work has been done with biquaternions, and I do not deny the validity of any of it.  Much effort has been directed toward "other hyper-complex numbers", such as Clifford algebras.  For the record, I am making a choice to focus on quaternions for reasons outlined by Dirac.

Dirac took a Mobius transformation from complex analysis and tried to develop a quaternion analog.  The approach is too general, and must be restricted to graft the results to the Lorentz group.  I personally have found this approach hard to follow, and have yet to build a working model of it in Mathematica.  I needed something simpler :-)

Multiplication of complex numbers can be thought of as a rotation and a dilation.  Conway and Silberstein's proposals only have the rotation component.  An additional dilation term might allow quaternions to do the necessary work.

C. Möller wrote a general form for a Lorentz transformation using vectors ("The Theory of Relativity", QC6 F521, 1952, eq. 25). For fixed collinear coordinate systems:

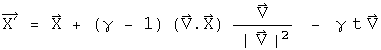
If V is only in the i direction, then

The additional complication to the X' equation handles velocities in different directions than i.

This has a vector equation and a scalar equation.  A quaternion equation that would generate these terms must be devoid of any terms involving cross products.  The symmetric product (anti-commutator) lacks the cross product;

Möller's equation looks like it should involve two terms, one of the form AqA (a rotation), the other Bq (a dilation).

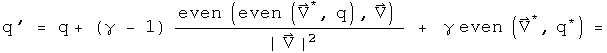
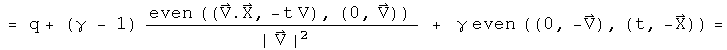
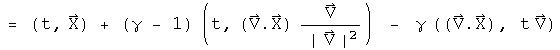
This is the general form of the Lorentz transformation presented by Möller.  Real quaternions are used in a rotation and a dilation to perform the work of the Lorentz group.

Is this result at all interesting?  A straight rewrite of Möller's equation would have been dull.  What is interesting is the equation which generates the Lorentz transformation.  Notice how the Lorentz transformation depends linearly on q, but the generator depends on q and q*.  That may have interesting interpretations.  The generator involves only symmetric products.  There has been some question in the literature about whether special relativity handles rotations correctly.  This is probably one of the more confusing topics in physics, so I will just let the observation stand by itself.

Two ways exist to use quaternions to do Lorentz transformations (to be discussed in the next web page).  The other technique relies on the property of a division algebra.  There exists a quaternion L such that:

For a boost along the i direction,

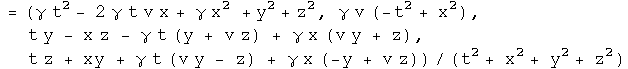
The quaternion L depends on the velocity and can depend on location in spacetime (85% of the type of problems assigned undergraduates in special relativity use an L that does not depend on location in spacetime).  Some people view that as a bug, but I see it as a modern feature found in the standard model and general relativity as the demand that all symmetry is local.  The existence of two approaches may be of interest in itself.